Introduction
Tile-based backgrounds are very common in 2d styled games. They're not only common in old games but also preferred in newer ones to give the game a special charme from the old days. I'll try to show you the mathematics behind this undertaking and give you all the stuff to implement this by yourself.
What is a tile?
A tile is rectangular or isometric image that is used to build a larger map. Many tiles are put together to form a bigger image like an element of a game for example a tree, and in the end the whole level. So that's where the name tile-based games comes from. The whole game is based on tiles. But in this example we would like to build a tile map that will function as our background for the start screen or menu.
Theory
First, let us visualize our current situation on the screen (black rounded rectangle):
I made up a coordinate system on the screen or window where I'm going to draw the tiled background. The coordinate system is the foundation for our next calculations. The horizontal axis (x-axis) runs from zero to window width in pixels; and the vertical axis (y-axis) runs from zero to window height in pixels. Additionally I placed a imaginary grid (gray lines) into it to represent the tiles. The cell size in this image was chosen at random but depends on the actual tile size.
Number of tiles
The first question is: How many tiles can we put in one row and how many can we put in one column?
The answer is easy if we look at the previous image. The calculation for this depends on the window, and tile size:
where m is the number of tiles on the horizontal axis; and n declares the number of tiles on the vertical axis. The other variables are self-explanatory. In this case we're also taking the ceiling function to round up the number. We don't mind if the tile images at the edges of the window are not fitting fully in one cell of the grid. If you don't want that you have to choose the tile size accordingly to your window size.
Example: If you screen size is 640x480, and every tile has a size of 80x80 then tiles are drawn horizontally and
tiles are drawn vertically. All in all 48 tiles will be visible on the screen.
Position of tiles
Given the two functions we can parametrize the position
for the tiles as follows:
with
You can see that we only accept discrete (integer) values. The positon depends on the parameters and
as well as the tile size which is constant. That makes sense? You'll see shortly what these parameters are for.
I should point out about what position I'm actually talking. This position describes the upper left corner of a tile. I have chosen this corner because most (if not all) graphic libraries out there are defined in that way if you want to draw 2d images. You specify exactly this corner and additionally the width and height of the image. So the only absolute position we need for the image to be drawn on the window is the upper left corner.
Finally, we can define the position of the tiles by this vector-valued function:
Algorithm for the tile map
Based on our previous foundations we now can build up the tile map. Visually it's a grid but it can be stored as an array. I'll use this as an advantage because accessing elements of a matrix can be more time consuming than on an array on certain circumstances. I'm sure that this can make huge differences especially for big tile maps (of course there are many more optimization techniques for that).
We can create the -grid background as follows:
That's it. We let each index run from zero to , respectively
. Index
is used for the position on the horizontal axis and index
for the position on the vertical axis. By that we get the correct position for each tile which can then be used for drawing.
Accessing the tile array
The tile map is stored as an array as mentioned before. I didn't told you yet how to access one concrete tile by specifing the i,j indizes like it was a matrix. Of course this isn't important when you only want to fill the background with the same tile. Then you don't need to store the image in an array, the tile image is probably stored in a variable that you access every time.
Assume you have a 1D array of length where all the different tile images are stored. To access a specific tile by
and
:
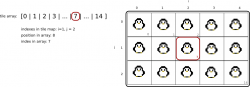
An example illustrates this in the following figure:
The numbers in the array represent the index position of the elements (tile images in this case)
When the algorithmus hits the index then the eighth element of the tile array is accessed at index
. This assumes that your array starts at index 0.
You have to incorporate that piece in the algorithm to pick the correct tile image from the array.
Closer Look
The drawing is realised row-wise. An example will make the procedure clear. I'll simulate the two first steps and then an arbitrary one.
Imagine our tile size is pixel. Let
, and
, then the position of the first tile is
. Then index
is incremented by one
, so the position of the second tile is
. The current situation is depicted below:
 Cute Retro Pixel Penguin 16x16 from 'NicoleMarieProductions'
Cute Retro Pixel Penguin 16x16 from 'NicoleMarieProductions'
The position for the ninth tile in the grid at would be
:
Cute Retro Pixel Penguin 16x16 from 'NicoleMarieProductions'
As you could see the indexes indicate the position in the grid (tile map) which is defined by and
. The function
translates them into pixel screen coordinates. So we can say the function performs a mapping of our imaginary grid coordinates to pixel screen coordinates.
Example in Irrlicht
Here is the source code for Irrlicht:
#include <irrlicht.h>
using namespace irr;
using namespace core;
using namespace scene;
using namespace video;
static int imageWidth;
static int imageHeight;
int* calculatePosition(int x, int y) {
int pos[2] = { x*imageWidth, y*imageHeight };
return pos;
}
int main() {
IrrlichtDevice *device =
createDevice(EDT_OPENGL, dimension2d(640, 480), 16, false, false, false, 0);
if (!device)
return 1;
device->setWindowCaption(L"Offbeat-Pioneer.net - Tile-based Background");
IVideoDriver* driver = device->getVideoDriver();
ISceneManager* smgr = device->getSceneManager();
// Credit for the image of retro pixel penguin goes to 'NicoleMarieProductions' (http://opengameart.org/content/cute-retro-pixel-penguin-16x16)
ITexture* penguin = driver->getTexture("./penguin.png");
int n; int m;
int screenWidth; int screenHeight;
//Retrieve screen, and tile size
screenWidth = driver->getScreenSize().Width;
screenHeight = driver->getScreenSize().Height;
imageWidth = penguin->getSize().Width;
imageHeight = penguin->getSize().Height;
//Calculate the number of tiles per row/column
n = ceil(screenHeight / imageHeight);
m = ceil(screenWidth / imageWidth);
while (device->run()) {
driver->beginScene(true, true, SColor(128, 128, 128, 100));
smgr->drawAll();
//Build up the tile map for the background
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= m; j++) {
int* pos = calculatePosition(j, i);
driver->draw2DImage(penguin, position2d(pos[0], pos[1]));
}
}
//for (int k = 0; k < n*m; k++) {
// int i = k % m;
// int j = floor(k / m);
// int* pos = calculatePosition(i, j);
// driver->draw2DImage(penguin, position2d(pos[0], pos[1]));
//}
driver->endScene();
}
return 0;
}The result:
This formulation of a tile-based background should be applicable in any other programming language.